3.4 Distribuciones de probabilidad
Es frecuente querer crear vectores que sigan una determinada distribución de probabilidad. Puede hacerse así:
x.uniforme <- runif(10)
x.normal <- rnorm(13)
Casi todas las distribuciones admiten parámetros adicionales. Por ejemplo, la media y la desviación estándar para la distribución normal. Consulta la ayuda de rnorm para ver cómo muestrear una variable aleatoria normal con media 1 y desviación estándar 3. Extrae una muestra del 10000 elementos de ella y comprueba que lo has hecho correctamente usando las funciones mean y sd.
Para entender la forma de esas distribuciones, podemos construir el histograma de una muestra, como a continuación:
hist(rnorm(1000))
hist(runif(1000))
hist(rpois(1000, 5))Busca cómo muestrear la distribución gamma.
Consulta la ayuda de rnorm, runif y rpois. ¿Qué tienen en común?
El ejercicio anterior debería poner de manifiesto cómo en R, asociada a cada distribución de probabilidad hay cuatro funciones cuyos nombres comienzan por las letras r, p, d y q. La función que comienza por r sirve para muestrear la distribución, como en los ejemplos anteriores.
La función que comienza por d es la densidad15 de la distribución. Por ejemplo, la función dnorm es la famosa campana de Gauss. Se puede representar con la función curve:
curve(dnorm(x, 0, 2), -8, 8)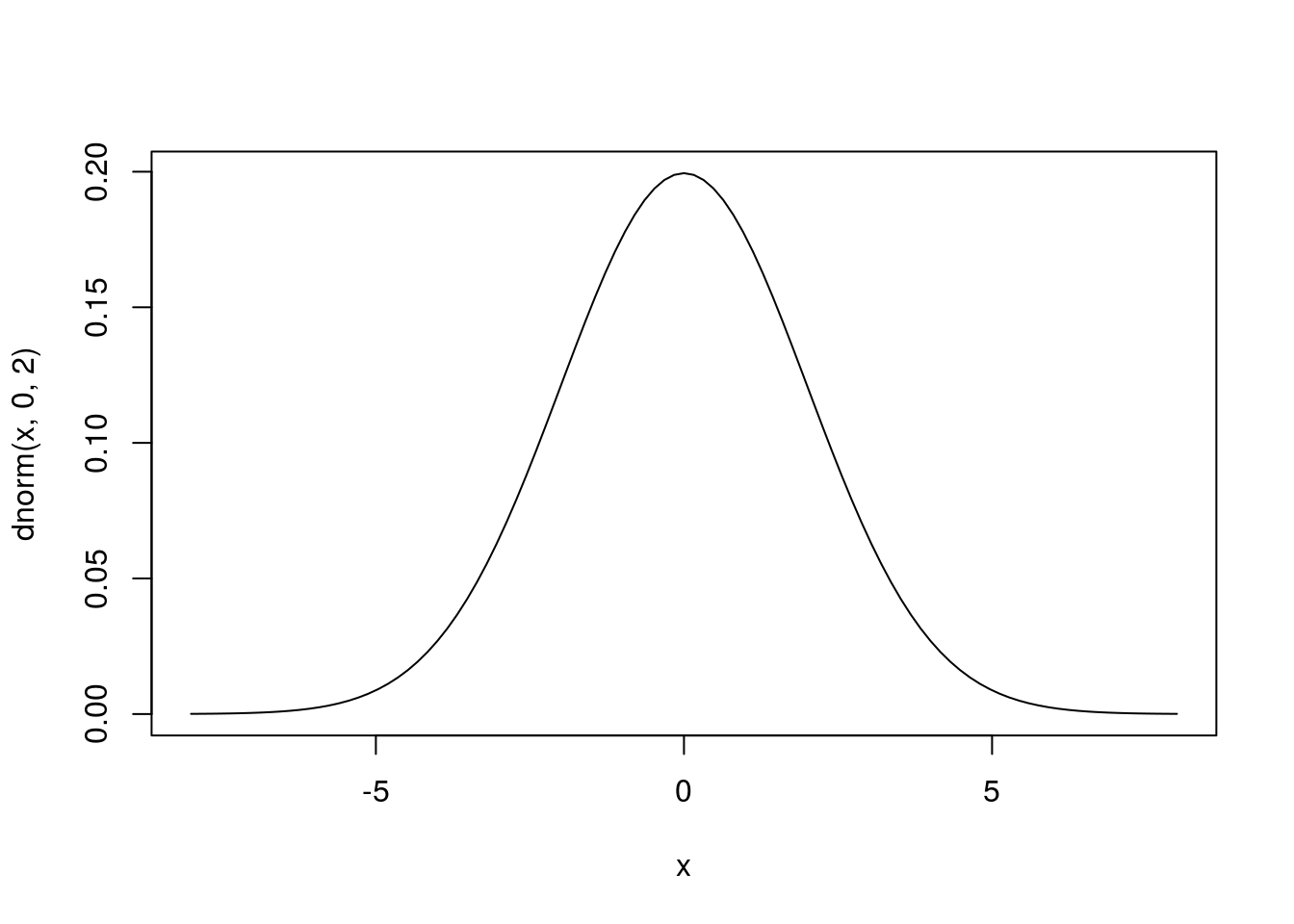
Usa curve para representar la densidad de la distribución beta para diversos valores de sus parámetros. Lee ?curve para averiguar cómo sobreimpresionar curvas y representa la densidad para diversas combinaciones de los parámetros con colores distintos. Puedes comparar el resultado con los gráficos que aparecen en la página de la distribución beta en la Wikipedia.
La función que comienza por p es la función de probabilidad, que es la integral de la densidad. En concreto, si la función de densidad es \(f\), la función de probabilidad, \(F\), es
\[ F(x) = \int_{-\infty}^x f(x) dx. \]
Como consecuencia, es una función que crece más o menos suavemente de 0 a 1.
curve(pnorm(x, 0, 2), -8, 8)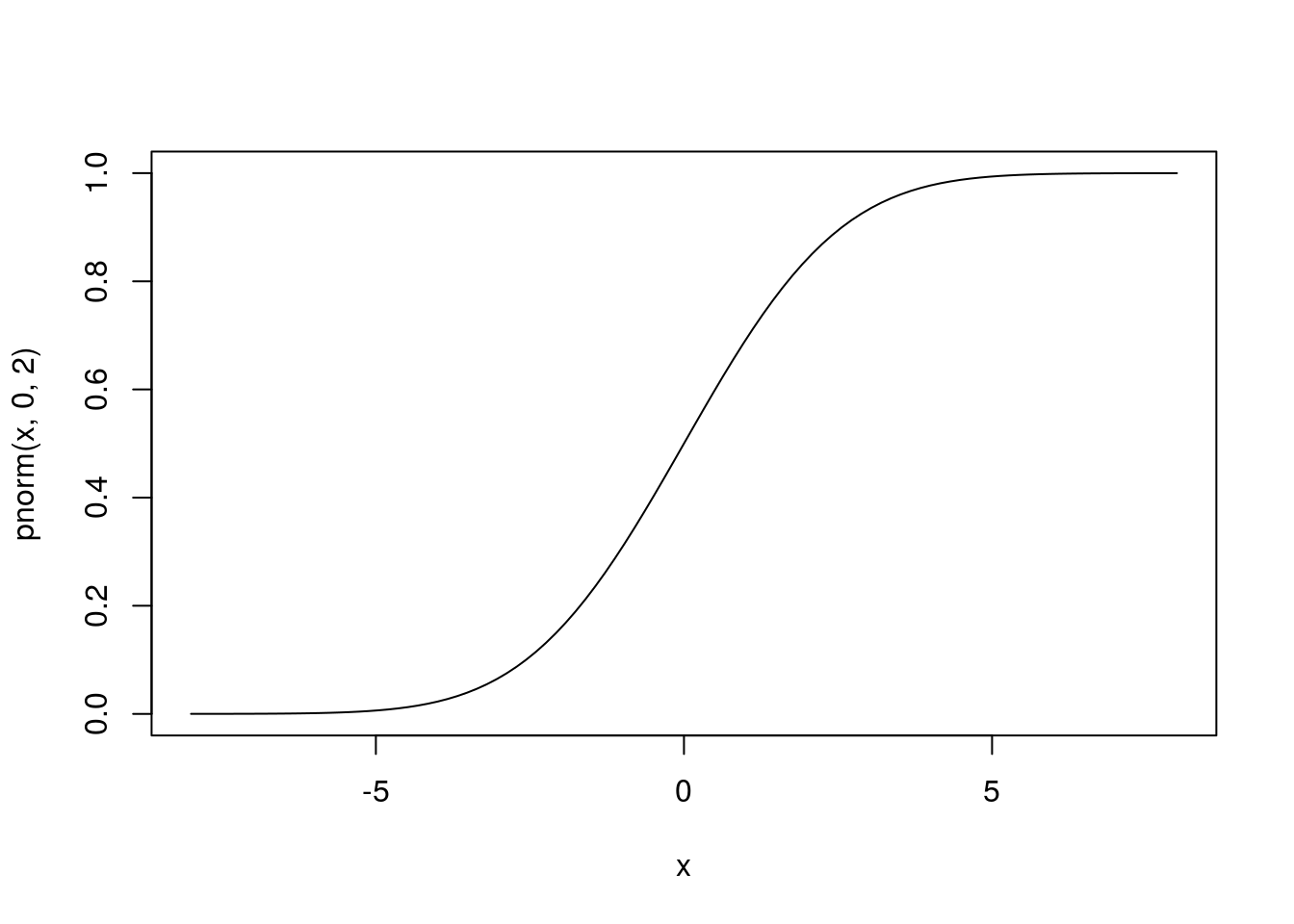
Finalmente, la función cuyo nombre comienza por q es la que calcula los cuantiles. Es decir, es la inversa de la función de probabilidad. Por ejemplo, en el gráfico
curve(dnorm(x, 0, 2), -8, 8)
abline(v = qnorm(0.1, 0, 2), col = "red")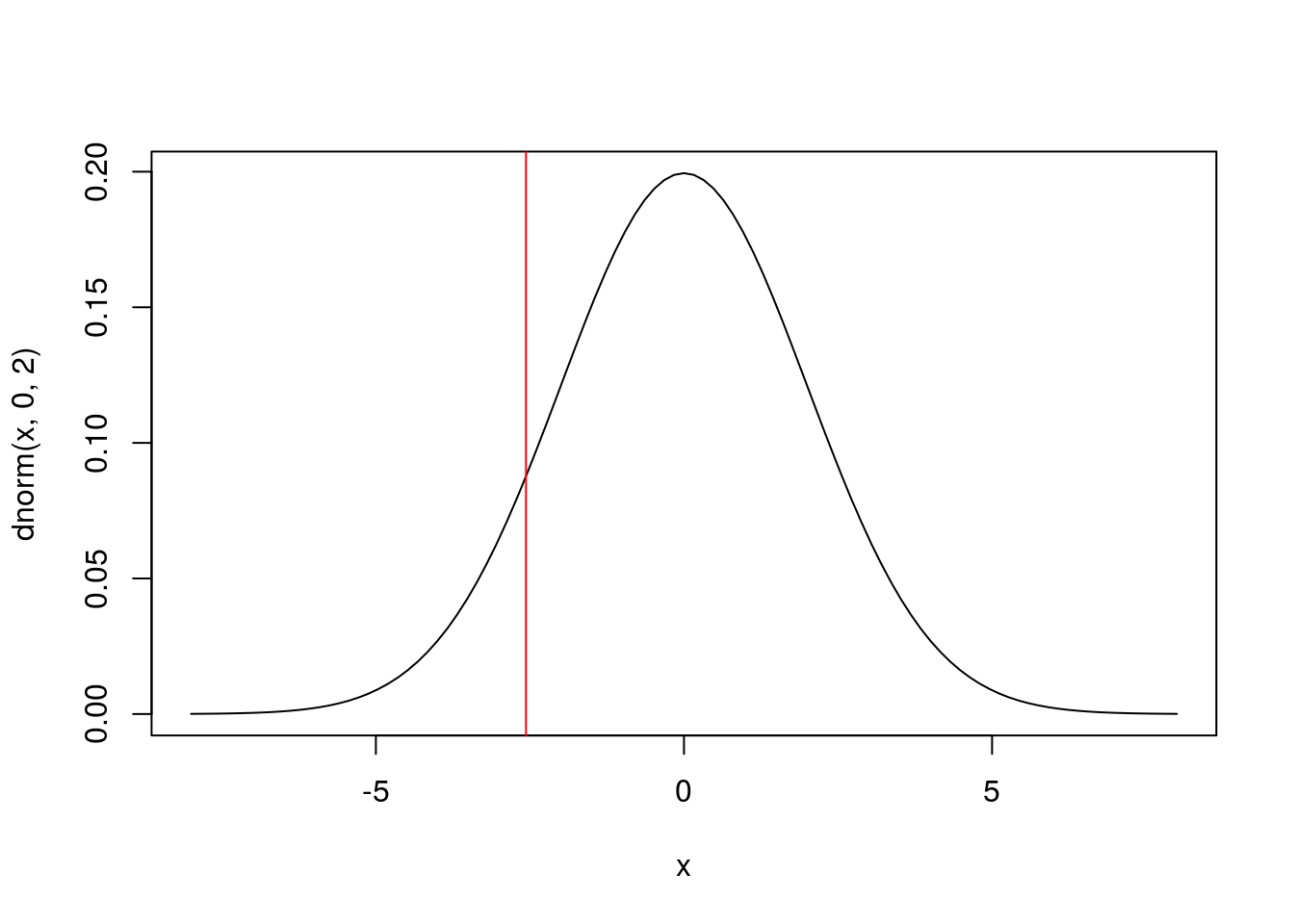
la probabilidad que asigna la normal a la zona que queda a la izquierda de la recta vertical roja es del 10%, valor indicado por el primer argumento de qnorm, 0.1.
Los conceptos de función de densidad, de probabilidad, etc. son muy importantes, aunque no para lo que sigue en el libro; si estás familiarizado con ellos, te servirá lo que sigue. Si no, puedes ignorarlo en una primera lectura.↩